Sudoku-Rating DE

Strategien und Techniken zur Lösung von Sudoku-Puzzles

Auf dieser Seite finden Sie Beschreibungen der Strategien, die man zur Lösung von Sudoku-Puzzles einsetzen kann.

Die Basisstrategien dienen dazu, den Wert für ein Feld im Sudoku-Puzzle zu bestimmen.

Reichen die Basisstrategien zur Lösung eines Puzzles nicht aus, kann man die Kandidaten-Strategien einsetzen, um Kandidaten für einzelne Felder auszuschließen.

Nach der Anwendung der Kandidaten-Strategien kann man meistens mit den Basisstrategien einzelne Felder setzen. Manchmal ist es aber auch notwendig, Kandidaten-Strategien mehrfach hintereinander anzuwenden, bevor man den Wert eines Feldes bestimmen kann.

Nicht alle Sudoku-Puzzles lassen sich mit den hier angeführten Strategien lösen.

Die Kriterien für die Einstufung einzelner Strategien und eine Statistik über die Häufigkeit von deren Verwendung findet sich auf der rating-Seite.

Basisstrategien

Nach meiner Ansicht gibt es nur zwei Strategien zum Bestimmen von Werten von einzelnen Felder. Alle anderen sind davon abgeleitet. Im Gegensatz zum Computer ist es dem Menschen jedoch möglich, in bei der Lösung von Puzzles mehrere Strategien zu kombinieren, um schneller ans Ziel zu kommen.

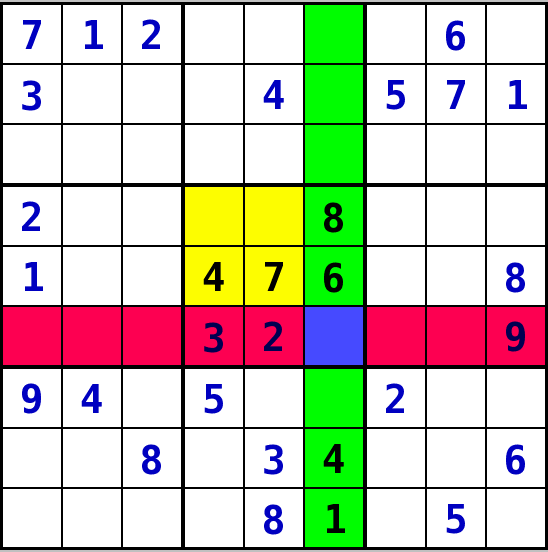Ein Feld, eine mögliche Zahl (Strategie 1)

Diese Strategie basiert darauf, dass für ein Feld nur noch ein Wert möglich ist, da die mit diesem Feld zusammenhängenden Bedingungsumfelder ( Spalte, Reihe, Block ) alle anderen Werte verwendet haben.

Kandidatenliste für das blaue Feld: 5

Von der Spalte verwendet: 1, 4, 6, 8

Von der Reihe verwendet: 2, 3, 9

Vom Block verwendet: 2, 3, 4, 6, 7, 8

Auf das Bild KLICKEN um es zu vergrößern!

Seitenanfang

Ein Bedingungsumfeld, eine Zahl nur in einem Feld möglich (Strategie 2)

Diese Strategie basiert darauf, dass für in einem Bedingungsumfeld (Spalte, Reihe, Block) ein Wert nur noch in einem Feld dieses Bedingungsumfeldes stehen kann.

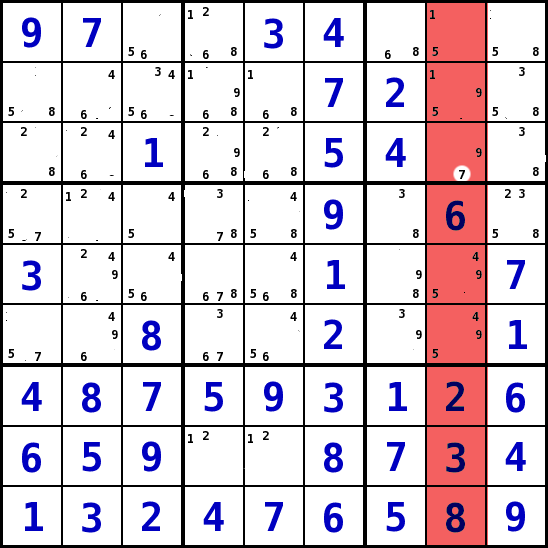
In diesem Beispiel wird die Spalte 8 betrachtet. In dieser Spalte kann d Wert 7 nur in Reihe 3 stehen. Damit muss die 7 in das Feld Spalte 8, Reihe 3 (S8R3).

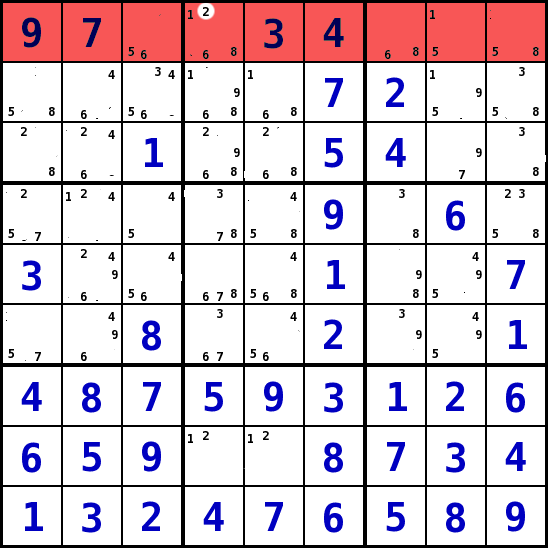
In diesem Beispiel wird die Reihe 1 betrachtet. In dieser Reihe kann die Zahl 2 nur in Spalte 4 stehen. Damit muss die 2 in das Feld Spalte 4, Reihe 1 (S4R1).

Auf das Bild KLICKEN um es zu vergrößern!

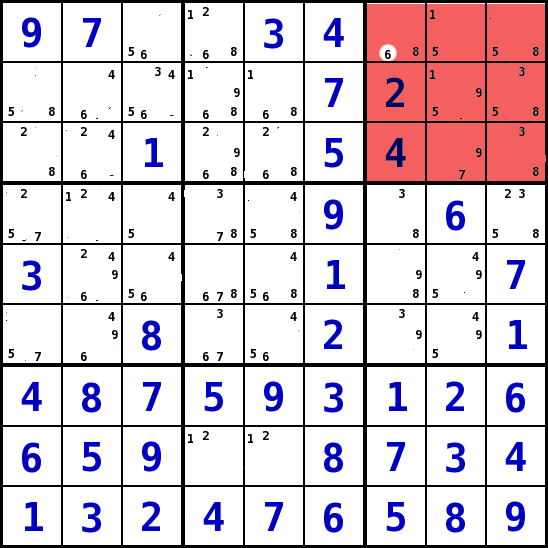
In diesem Beispiel wird der Block 3 betrachtet. In diesem Block kann die Zahl 6 nur in Spalte 7 in der Reihe 1 stehen. (S7R1).

Auf das Bild KLICKEN um es zu vergrößern!

Seitenanfang

Kandidaten-Strategien

Die Kandidaten-Strategien dienen dazu, die möglichen Kandidaten für ein Feld zu vermindern. Man möchte mit der Anwendung dieser Strategien erreichen, die Kandidaten soweit einzuschränken, dass man mit den Basisstrategien zum Erfolg kommt.

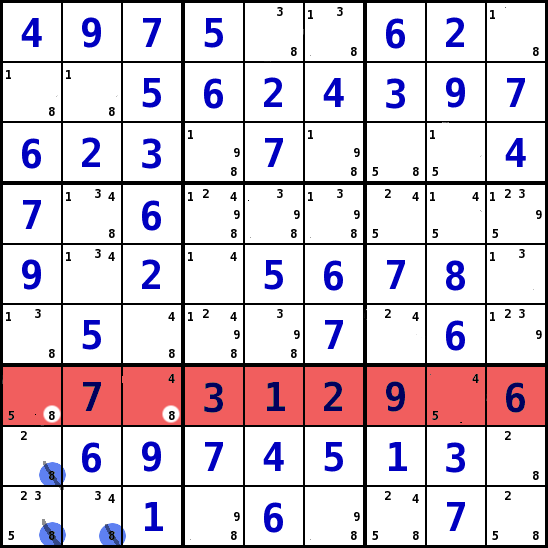Eine Linie, ein Wert nur in einem Block (Strategie 3)

Diese Strategie betrachtet jeweils eine Linie , d.h. entweder eine Spalte oder Reihe. Wenn man eine Linie findet, bei der ein Wert nur in einem Block der drei Blöcke liegen kann, die diese Linie durchläuft, so kann man sagen, dass dieser Wert in den anderen Feldern dieses einen Blockes nicht mehr vorkommen kann.

In der Reihe 7 des Beispiels kann der Wert 8 nur im ersten Block stehen, den diese Reihe durchläuft. Aus diesem Grund muß die 8 in Feld 1 oder 3 dieses Blocks stehn. In den Feldern 8 und 9 der Spalte 1 (S1R8, S1R9) , und dem Feld 9 der Spalte 2 (S2R9) kann man also die 8 als Kandidaten entfernen.

Auf das Bild KLICKEN um es zu vergrößern!

Seitenanfang

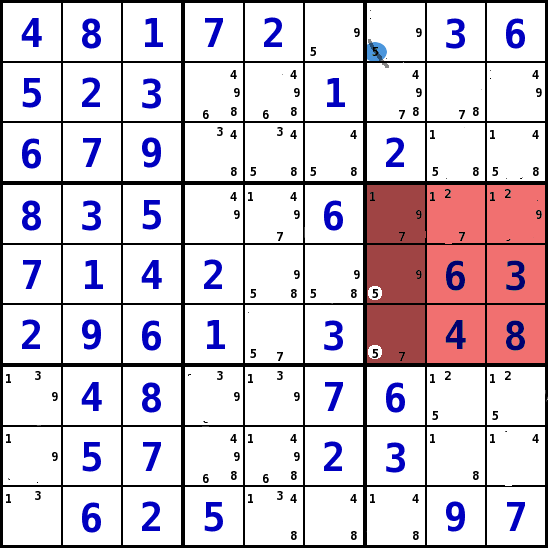Ein Block , ein Wert nur in einer Linie (Strategie 4)

Diese Strategie betrachtet jeweils einen Block. Wenn man einen Block findet, bei dem ein Wert nur in einer Linie (Spalte/Reihe) dieses Blockes liegen kann, so kann man sagen, dass dieser Wert in den anderen Feldern dieser Linie, die nicht in diesem Block liegen, nicht mehr vorkommen kann.

Im Block 6 des Beispiels kann der Wert 5 nur in der siebten Spalte des Spielfeldes liegen. Deswegen kann ist der Wert 5 kein Kandidat mehr für die Felder dieser Spalte, die nicht in diesem Block sind. Aus diesem Grund kann man die 5 als Kandidat im Feld Spalte 7 Reihe 1 (S7R1) streichen.

Auf das Bild KLICKEN um es zu vergrößern!

Seitenanfang

Strategien mit zwei Werten und zwei Feldern (Strategie 5)

Das Level 5 vereinigt zwei Strategien, die auf 2 Feldern mit 2 möglichen Werten beruhen. Die eine basiert auf offensichtlichen Kombinationen von zwei Kandidaten-Werten mit zwei Feldern, die andere basiert auf einer versteckten Kombination von zwei Werten und zwei Feldern.

Diese Strategien beziehen sich jeweils auf ein Bedingungsumfeld (Spalte, Reihe, Block).

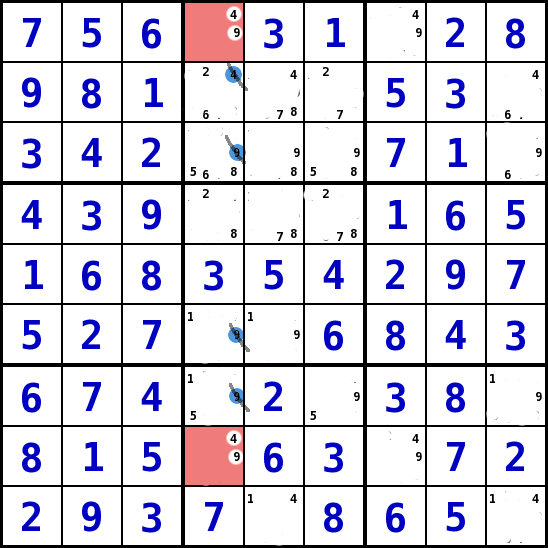Ein Bedingungsumfeld , zwei Felder mit zwei Kandidaten (Strategie 5)

Diese Strategie betrachtet jeweils eine Bedingungsumfeld (Spalte, Reihe, Block). Gesucht werden Felder mit genau 2 Kandidaten-Werten. Findet man zudem 2 Felder mit genau den gleichen Kandidaten-Werten in der gleichen Reihe/Spalte oder dem gleichen Block, so sind diese beiden Werte in keinem anderen Feld dieser Reihe/Spalte bzw. dieses Blocks möglich.

In der Spalte 4 des Beispiels sind in Reihe 1 und 8 (S4R1, S4R8) nur die Werte 4 und 9 möglich. Das heiß , dass sie hier stehen müssen. Daraus kann man schließen dass in keinem anderen Feld dieser Spalte die Werte 4 und 9 stehen können.

Wir können also diese Werte aus den Feldern Reihe 2, 3, 6, 7 der Spalte 4 (S4R2, S4R3, S4R6, S4R7), diese Werte als Kandidaten streichen.

Auf das Bild KLICKEN um es zu vergrößern!

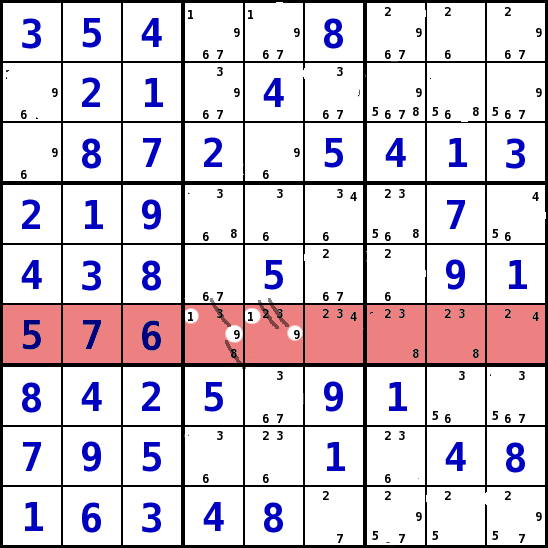Ein Bedingungsumfeld, zwei Werte können nur in zwei Feldern stehen (Strategie 5)

Bei dieser Strategie geht es darum, in einem Bedingungsumfeld (Spalte, Reihe, Block) nach Kombinationen von zwei Kandidaten-Werten zu suchen, die nur in zwei Feldern dieses Bedingungsumfeldes stehen können.

Hat man eine solche Kombination gefunden, kann man sagen, dass diese zwei Werte in diesen beiden Feldern stehen müssen. Das heißt, dass man in diesen Feldern alle anderen Kandidaten entfernen kann.

In dem Beispiel können in der sechsten Reihe die Werte 1 und 9 nur in den Spalten 4 und 5 stehen (S4R6, S5R6). Deshalb können hier keine anderen Werte stehen und man kann alle Kandidaten-Werte außer 1 und 9 aus diesen Feldern entfernen.

Seitenanfang

Strategien mit drei Werten und drei Feldern (Strategie 6)

Das Level 6 vereinigt zwei Strategien, die auf 3 Feldern mit 3 möglichen Werten beruhen. Die eine basiert auf offensichtlichen Kombinationen von drei Kandidaten-Werten mit drei Feldern, die andere basiert auf einer versteckten Kombination von drei Werten und drei Feldern.

Diese Strategien beziehen sich jeweils auf ein Bedingungsumfeld (Spalte, Reihe, Block).

Die Strategien des Level 6 sind im Prinzip die gleichen wie in Level 5, nur dass sie mit 3 Feldern und 3 Werten arbeiten.

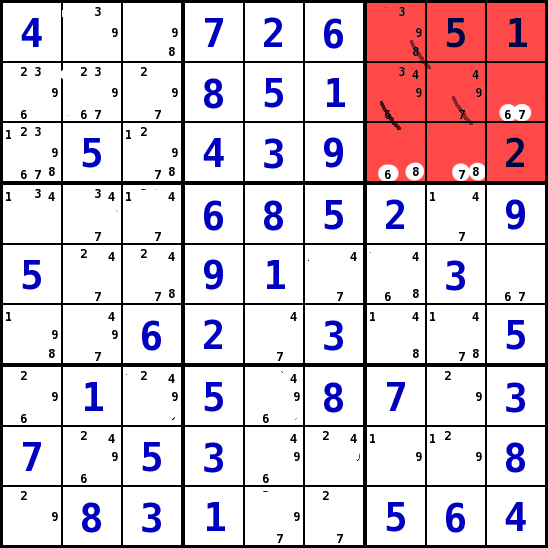Ein Bedingungsumfeld , drei Felder mit zusammen drei Kandidaten (Strategie 6)

Diese Strategie betrachtet jeweils eine Bedingungsumfeld (Spalte, Reihe, Block). Gesucht werden Felder mit 2 bis 3 Kandidaten-Werten. Findet man 3 Felder mit insgesamt drei gemeinsamen Kandidaten-Werten in der gleichen Reihe/Spalte oder dem gleichen Block, so sind diese beiden Werte in keinem anderen Feld dieser Reihe/Spalte bzw. dieses Blocks möglich.

Im Block 3 des Beispiels sind in der Spalte 7 Reihe 3 (S7R3), Spalte 8 Reihe 3 (S8R3) und Spalte 9 Reihe 2 (S9R2) zusammen nur die Werte 6, 7 und 8 möglich. Das heiß , dass sie in diesen Feldern stehen müssen. Daraus kann man schließen dass in keinem anderen Feld dieses Blocks die Werte 6, 7 und 8 stehen können.

Wir können also diese Werte aus den Feldern Spalte 7 Reihe 1 und 2 (S7R1, S7R2) und aus Spalte 8 Reihe 2 (S8R2) als mögliche Kandidaten entfernen.

Auf das Bild KLICKEN um es zu vergrößern!

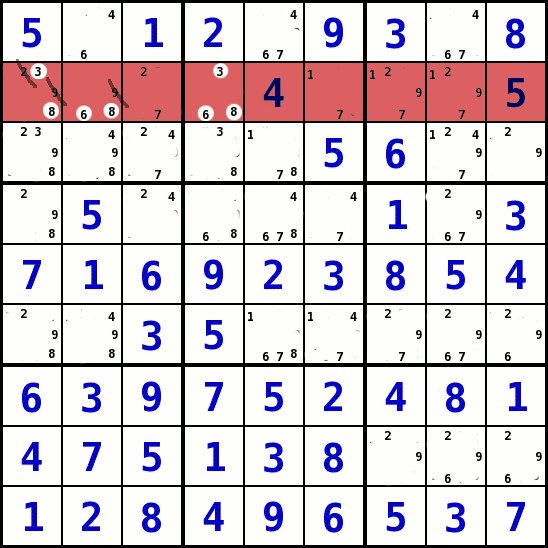Ein Bedingungsumfeld, drei Werte können nur in drei Feldern stehen (Strategie 6)

Bei dieser Strategie geht es darum, in einem Bedingungsumfeld (Spalte, Reihe, Block) nach Kombinationen von drei Kandidaten-Werten zu suchen, die nur in drei Feldern dieses Bedingungsumfeldes stehen können.

Hat man eine solche Kombination gefunden, kann man sagen, dass diese drei Werte in diesen beiden Feldern stehen müssen. Das heißt, dass man in diesen Feldern alle anderen Kandidaten entfernen kann.

In dem Beispiel können in der zweiten Reihe die Werte 3, 6 und 8 nur in den Spalten 1, 2 und 4 stehen (S1R2, S2R2, S4R2). Deshalb können hier keine anderen Werte stehen und man kann alle Kandidaten-Werte außer 3, 6 und 8 aus diesen Feldern entfernen.

Seitenanfang

Strategien mit vier Werten und vier Feldern (Strategie 7)

Das Level 7 vereinigt zwei Strategien, die auf 4 Feldern mit 4 möglichen Werten beruhen. Die eine basiert auf offensichtlichen Kombinationen von vier Kandidaten-Werten mit vier Feldern, die andere basiert auf einer versteckten Kombination von vier Werten und vier Feldern.

Diese Strategien beziehen sich jeweils auf ein Bedingungsumfeld (Spalte, Reihe, Block).

Die Strategien des Level 7 sind im Prinzip die gleichen wie in Level 5, nur dass sie mit 4 Feldern und 4 Werten arbeiten.

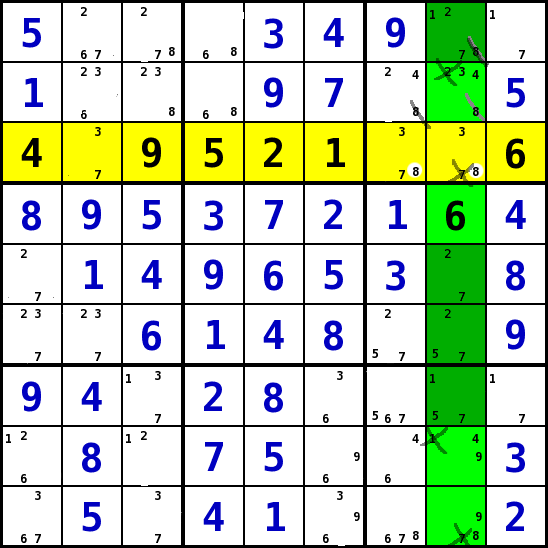Ein Bedingungsumfeld , vier Felder mit zusammen vier Kandidaten (Strategie 7)

Diese Strategie betrachtet jeweils eine Bedingungsumfeld (Spalte, Reihe, Block). Gesucht werden Felder mit 2 bis 4 Kandidaten-Werten. Findet man 4 Felder mit insgesamt vier gemeinsamen Kandidaten-Werten in der gleichen Reihe/Spalte oder dem gleichen Block, so sind diese beiden Werte in keinem anderen Feld dieser Reihe/Spalte bzw. dieses Blocks möglich.

In dem Beispiel wurde zuerst die Strategie des level 3 auf die dritte Reihe (gelb) angewendet um den Wert 8 in den Feldern Spalte 7 Reihe 2 (S7R2) und Spalte 8 Reihe 1 und 2 (S8R1, S8R2) als Kandidaten auszuschließen.

In der Spalte 8 des Beispiels haben die Felder in den Reihen 1, 5, 6 und 7 (S8R1, S8R5, S8R6,S8R7) zusammen die vier Kandidaten-Werte 1, 2, 5 und 7. Daraus kann man schließen, dass diese Werte in keinem anderen Feld dieser Spalte Kandidaten-Werte sein können.

So kann man den Wert 7 aus den Feldern in Reihe 3 und 8 (S8R3, S8R8) , den Wert 1 aus der Reihe 8 (S8R8), und den Wert 2 aus der Reihe 2 (S8R2) als Kandidaten entfernen.

Auf das Bild KLICKEN um es zu vergrößern!

Ein Bedingungsumfeld, vier Werte können nur in vier Feldern stehen (Strategie 7)

Bei dieser Strategie geht es darum, in einem Bedingungsumfeld (Spalte, Reihe, Block) nach Kombinationen von vier Kandidaten-Werten zu suchen, die nur in vier Feldern dieses Bedingungsumfeldes stehen können.

Hat man eine solche Kombination gefunden, kann man sagen, dass diese vier Werte in diesen beiden Feldern stehen müssen. Das heißt, dass man in diesen Feldern alle anderen Kandidaten entfernen kann.

Für diese Strategie sollte es kein Beispiel geben, das nicht schon mit der vorherigen 4 Felder Strategie gelöst werden kann. Das liegt daran, dass ein Vorkommen eines verborgenen 4ers (aktuelle Strategie) einen offenen 5 (Strategie 14) erfordert. Diese kann aber nicht vorkommen, da sie von einen offenen 4er ( Strategie 7, erste Variante) bedingen würde. Wenn man systematisch vorgeht, ist dieser Fall damit schon abgedeckt, bevor diese Strategie zum Zuge kommen kann.

Seitenanfang

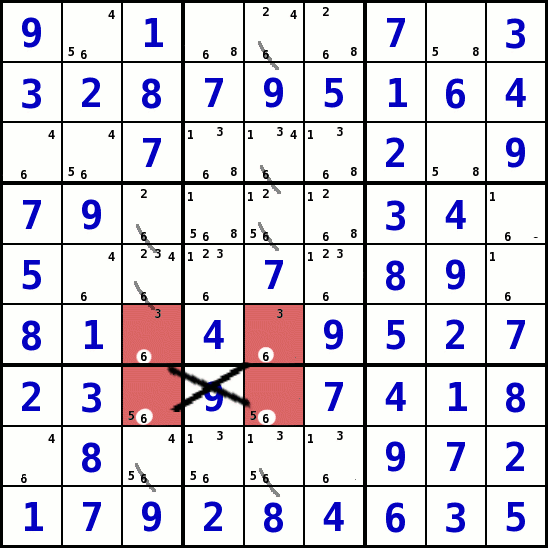Kreuzweise verbundene Felder : XWing (Strategie 8)

Die Idee dieser Strategie ist es, über kreuzweise verbundene Kandidaten-Werte Aussagen über andere Felder und Kandidaten-Werte zu machen. Man sucht in einem Bedingungsumfeld ( Spalte, Reihe, Block ) nach einem Kandidaten-Wert der nur in zwei Feldern möglich ist. Hat man eine solche Kombination gefunden, sucht man in den restlichen Spalten, Reihen und Blöcken nach dem selben Wert und überprüft, ob er dort auch nur an zwei Stellen sein kann. Hat man eine solche Konstellation gefunden, wird als letztes überprüft, ob diese vier Felder in denen dieser Werte vorkommen kann, die Kombination von 2:2:x der Bedingungsumfeld-Kategorien (Spalte, Reihe, Block) benutzen, d.h. z.B. 2 Blöcke, 2 Reihen, beliebig viele Spalten. Hat man eine solche Kombination gefunden kann man aussagen, dass der gemeinsame Kandidaten-Wert der vier Felder nicht in den restlichen Feldern der Spalten/Reihen/Blöcke der 2er-Kombinationen stehen können.

VIEL THEORIE !!!

Im Beispiel kann der Wert 6 nur in den Reihen 6 und 7 nur in zwei Spalten stehen. In beiden Reihen sind es die Spalten 3 und 5 (S3R6, S5R6, S3R7, S5R7). In diesem Fall haben wir 2 Reihen, 2 Spalten und 4 Blöcke ( 2:2:x). Es besteht ein gedachtes Kreuz der Abhängigkeit. Wenn in S3R6 eine 6 stehen würde müßte in S5R7 eine 6 stehen. Entsprechend für S5R6 und S3R7. Damit wird klar, dass der Wert 6 für diese beiden Spalten in einer dieser Reihen stehen muss.

Aus diesem Grund kann man in den gemeinsamen Spalten 3 und 5 in allen Feldern die nicht in diesen Reihen stehen die 6 als Kandidaten entfernen.

Auf das Bild KLICKEN um es zu vergrößern!

Seitenanfang

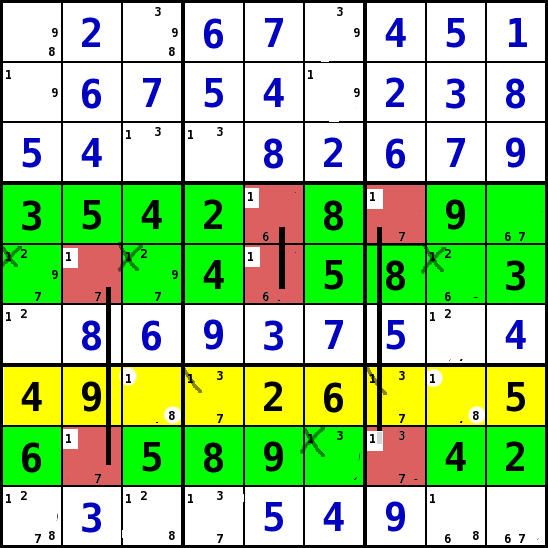Verbundene Felder über 3 Bedingungsumfelder: Swordfish (Strategie 9)

Die Idee dieser Strategie ist eine Erweiterung der XWing-Strategie die sich nun aber auf drei Bedingungsumfelder bezieht. Aussagen über andere Felder und Kandidaten-Werte zu machen. Man versucht nach Kandidaten-Werten die in mindestens drei Bedingungsumfeldern 2 oder 3 mal möglich sind. Kann manfür einer Kandidaten-Wert die Felder in denen er in drei verschiedenen Bedingungsumfeldern möglich ist, so verbinden, dass sie genau 3 Bedingungsumfelder einer anderen "Richtung" belegen, so kann man sagen, dass dieser Wert in einem der Felder liegen muss, die gewählt wurden. In anderen Feldern, die von von mindestens zwei dieser Felder gemeinsam beeinflusst werden, kann der Kandidatenwert nicht vorkommen.

Eine solche Konstellation bedeutet dass die 6 - 9 Felder, die daran beteiligt sind die Kombination von 3:3:x der Bedingungsumfeld-Kategorien (Spalte, Reihe, Block) benutzen, d.h. z.B. 3 Blöcke, 3 Reihen, beliebig viele Spalten. Ist eine solche Kombination gefunden kann man aus den Bedingungsumfeldern in den Kategorien die jeweils 3 mal benutzt werden, den Wert als Kandidat aus allen Felden entfernen, die nicht Bestandteil der Kombinationsmatrix ist.

VIEL THEORIE !!!

START: Zuerst wurde mit Hilfe der Strategie level 5, in der Reihe 7 (gelb) der Wert 7 in den Spalten 4 und 7 (S4R7, S7R7) als Kandidaten entfernt.

In dem Beispiel kann jetzt der Wert 1 in den Spalten 2, 5 und 7 nur noch in jeweils 2 Feldern stehen ( rote Felder, schwarze Balken, S2R5, S2R8, S5R4, S5R5, S7R4 und S7R8)

Wenn man diese 3 mal 2 Felder querverbindet ( grün) erkennt man, dass sie insgesamt 3 Reihen, 3 Spalten und 5 Blöcke belegen (Regel 3:3:x) . Dadurch beeinflussen sich die Felder gegenseitig. Man kann festellen, dass die 1 in den grünen Reihen nur in den roten Feldern liegen können.

Man kann es auch durchspielen: Der Wert 1 kann in der Spalte 2 nur in den Reihen 5 und 8 liegen (S2R5, S2R8).

• Variante 1: Liegt der Wert 1 im Feld S2R5, gilt für Spalte 5 , dass der Wert 1 in Reihe 4 (S5R4) liegen muss, woraus sich ergibt dass in Spalte 7 der Wert 1 in Reihe 8 (S7R8) liegen muss. Belegte Reihen : 4, 5, 8
• Variante 2: Liegt der Wert 1 im Feld S2R8, gilt für Spalte 7 , dass der Wert 1 in Reihe 4 (S7R4) liegen muss, woraus sich ergibt dass in Spalte 5 der Wert 1 in Reihe 5 (S5R5) liegen muss. Belegte Reihen : 4, 5, 8

Daraus ergibt sich, dass immer die Reihen 4,5 und 8 von den ausgewählten Feldern abgedeckt werden. Daraus folgt, dass wir den Wert 1 als Kandidaten aus den restlichen Feldern dieser drei Reihen entfernen kann (S1R5, S3R5, S6R8, S8R5).

Auf das Bild KLICKEN um es zu vergrößern!

Seitenanfang

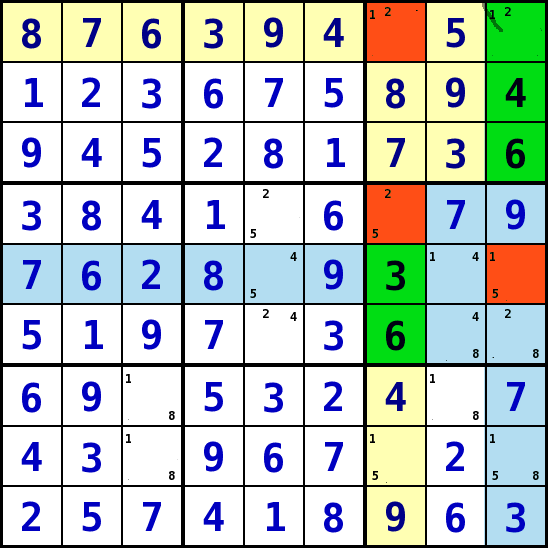3 Felder mit je zwei Kandidaten-Werten über Eck: XYWing (Strategie 10)

Die Idee dieser Strategie ist eine Fortsetzung der Strategie des level 6 ( drei Felder mit insgesamt 3 Kandidaten), die ja darauf zielt diese 3 Kandidaten-Werte im restlichen Bedingungsumfeld auszuschließen. Bei dieser neuen Strategie fällt die Bedingung, dass diese drei Felder in einem Bedingungsumfeld liegen müssen, weg. Damit ergibt sich natürlich die Notwendigkeit, die drei Felder über andere Bedingungen zu verknüpfen, um Aussagen machen zu können.

Folgende Bedingungen müssen erfüllt sein:

• Jedes Feld darf nur 2 Kandidaten-Werte haben.
• Alle drei Felder müssen zusammen genau drei unterschiedliche Kandidaten-Werte haben.
• Jedes Feld hat je einen gemeinsamen Kandidaten-Wert mit jedem der anderen Felder.
• Das mittlere Feld (der Verbinder) muss mit den beiden äußeren Feldern (Eckfeldern, Flügeln) über genau 1 Bedingungsumfeld (Spalte,Reihe,Block) verbunden sein.
• Die beiden Eckfelder dürfen kein gemeinsamens Bedingungsumfeld haben, sonst hätte man die selbe Situation, die schon in Strategie 6 abgedeckt wurde.

Hat man so eine Situation gefunden, hängen die Kandidaten-Werte der drei Felder zusammen. Setzt man den Wert in einem Feld bestimmen sich automatisch die Werte für die anderen beiden Felder.

Interessant ist hier der Kandidaten-Wert, den die beiden Eckfelder teilen. Da man sagen kann, dass dieser auf jeden Fall in einem der Eckfelder liegen muss. Da laut Bedingung beide Felder kein gemeinsames Bedingungsumfeld haben, stellt sich die Frage, wie diese Information helfen kann.

Selbst wenn zwei Felder des Spielfeldes kein gemeinsames Bedingungsumfeld habe, wirken sie dennoch auf 2 Felder gemeinsam ein, die Felder in denen sich ihre Bedingungsumfelder überschneiden.

Weiß man also, dass zwei Felder alternativ einen Wert enthalten müssen kann man diesen Wert als Kandidaten aus den Überschneidungsfeldern entfernen.

VIEL THEORIE !!!

In dem Beispiel werden die Felder Spalte 7 Reihe 1 und 4 (S7R1, S7R4) und Spalte 9 Reihe 5 (S9R5) betrachtet(rot). Jedes der Felder hat 2 Kandidaten-Werte, zusammen haben sie 3 Kandidaten-Werte (1, 2 und 5) und sie teilen je einen unterschiedlichen Kandidaten-Wert mit den beiden anderen Feldern:

• die Felder S7R1 und S7R4 haben den gemeinsamen Wert: 2
• die Felder S7R4 und S9R5 haben den gemeinsamen Wert: 5
• die Felder S7R1 und S9R5 haben den gemeinsamen Wert: 1

Das mittlere Feld (S7R4) hat je eine gemeinsames Bedingungsumfeld mit den Eckfeldern , mit S4R1 eine gemeinsame Spalte und mit S9R5 einen gemeinsamen Block. Sie bilden eine Kette. Die Eckfelder S7R1 und S9R5 haben keine gemeinsamen Spalten, Reihen, Blöcke.
Der Wert 1 ist gemeinsamer Kandidat für die Eckfelder und muss in einem dieser Felder stehen. Wenn in S7R4 der Wert 5 steht, steht der Wert 1 in S9R5, steht in S7R4 der Wert 2 , steht der Wert 1 in S7R1.

Wenn der Wert 1 entweder in Feld S7R1 oder S9R5 stehen muss, kann er nicht er nicht mehr ein Kandidat für die Felder sein, in denen sich die Bedingungsumfelder dieser zwei Felder (S7R1 (gelb), S9R5 (blau)) überschneiden( grün).
Darum kann man den Wert 1 als Kandidaten aus Feld S9R1 entfernen.

Auf das Bild KLICKEN um es zu vergrößern!

Seitenanfang

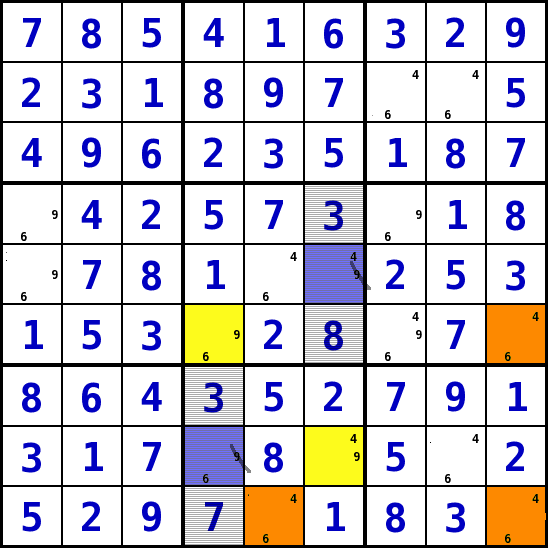XYWing mit einer Kette von Feldern als mittleres Element: XYWing with chain (Strategie 11)

Die Idee dieser Strategie ist eine Fortsetzung oder Erweiterung der Srategie 10. Neu daran ist dass es nicht mehr ein mittleres Feld gibt, das die beiden äußeren Felder verbindet, sondern eine Kette von Feldern mit 2 Kandidaten-Werten. Damit eine solche Kette eingesetzt werden kann, müssen 3 Bedingungen erfüllt sein:

• die benachbarten Felder der Kette sind jeweils über ein Bedingungsumfeld verbunden
• die Felder der Kette müssen alle die gleichen zwei Kandidaten haben
• die Kette muss eine ungerade Anzahl von Elementen haben (Strategie 10 ist der Spezialfall einer Kette mit einem Element).

Wenn die Kette aus einer ungeraden Anzahl von Feldern mit den gleichen Kandidaten-Werten besteht, kann man feststellen, dass die Enden der Kette immer synchron den gleichen Wert annehmen müssen.

Im Beispiel bilden die orangen Felder S5R9, S9R9 und S9R6 eine solche Kette. Nimmt S5R9 den Wert 6 an, hat auch S9R6 den Wert 6. Mit dieser Tatsache im Blick, kann man diese Kette wie ein Feld betrachten, wenn man nur die beiden Felder am Ende der Kette betrachtet.

Wie bei Strategie 10 sucht man jetzt für jedes Feld am Ende der Kette jeweils ein (Anschluss-)Feld, dass mit diesem über ein Bedingungsumfeld (Spalte, Reihe,Block) verbunden ist und nur einen gemeinsamen Kandidaten-Wert mit der Kette hat. Jedes dieser beiden Anschlussfelder muss exclusiv einen der Kandidaten-Werte der Kette haben. Hat die Kette die Kandidaten-Werte 6 und 4, so muss das eine Anschlussfeld den Kandidaten-Wert 6 und das andere den Kandidaten-Wert 4 haben.

Als letztes müssen die beiden Anschlussfelder einen gemeinsamen zweiten Kandidaten-Wert besitzen. Nur dann kann man eine Aussage machen (wie in Strategie 10).

Hat man alle anderen niedrigeren Strategien angewendet, kommt man nur dann zu neuen Aussagen, wenn die Anschlussfelder kein gemeinsames Bedingungsumfeld haben. Dies ist aber keine (programm)-technische Anforderung, sondern verhindert nur das Überprüfen von erfolglosen Kombinationen.

Wenn man dann diese beiden Felder, die über die Kette verbunden sind, betrachtet, kann man die "Kettenreaktion" verfolgen. Da die End-Felder der Kette, die beiden Kandidaten-Werte synchron annehmen, muss der gemeinsame Kandidaten-Wert der Anschlussfelder in einem der beiden Anschlussfelder stehen, je nach dem, welcher Wert jeweils von den Kettenenden angenommen wird.

Daraus kann man wiederum schließen, dass dieser Kandidaten-Wert nicht in den Feldern sein kann, den die beiden Anschlussfelder gemeinsam beeinflussen, d.h. in der Schnittmenge der Bedingungsumfelder dieser Felder ohne sie selbst.

VIEL THEORIE !!!

die Kette

In dem Beispiel besteht die Kette aus den orangen Feldern S5R9, S9R9 und S9R6 mit dem gemeinsamen Kandidaten-Werten 6 und 4.

die Anschlussfelder

Die Anschlussfelder S6R8 und S4R6 (gelb) teilen mit der Kette exclusiv die Kandidaten-Werte 4 (S6R8) und 6 (S4R6) und haben als gemeinsamen Kandidaten-Wert die 9.

die Logik

In allen Felder, die die beiden Anschlussfelder gemeinsam beeinflussen kann keine 9 stehen, da die Ketten-Enden (S5R9, S9R6) entweder gemeinsam den Wert 6 annehmen, dann muss der Wert 9 im Feld S6R8 stehen, oder die Ketten-Enden nehmen den Wert 4 an, dann muss der Wert 9 im Feld S4R6 stehen.

das Resultat

Die von den Anschlussfeldern gemeinsam beeinflussten Felder sind straffiert.
Die Felder, in denen der Kandidaten-Wert 9 ausgeschlossen wurde (S4R7, S6R4), sind blau gekennzeichnet.

Auf das Bild KLICKEN um es zu vergrößern!

Seitenanfang

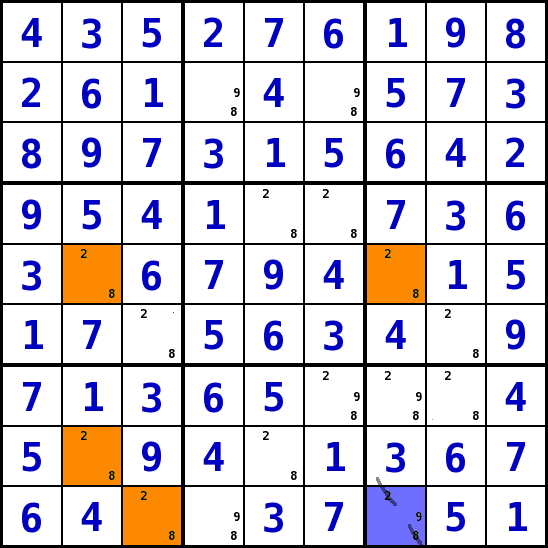Kette von Feldern mit zwei Kandidaten: EvenChain (Strategie 12)

Die Idee dieser Strategie ist eine Fortsetzung oder Erweiterung der Strategie 5 mit 2 Feldern in einem Bedingungsumfeld, die die gleichen 2 Kandidaten-Werte haben. Damit konnte man sagen, dass in dem Bedingungsumfeld, das diese beiden Felder teilen, diese beiden Kandidaten-Werte nicht in anderen Feldern möglich sind.

Die Idee dieser neuen Strategie ist es nun mehrere dieser 2 Feld-Kombinationen mit den gleichen Kandidaten-Werten darüber gemeinsame Felder zu verbinden, dass eine Kette von Feldern entsteht, die genau die gleichen Kandidaten-Werte besitzen. Die Werte, die die Felder einer solchen Kette annehmen ergibt sich, sobald man eines dieser Felder mit einem Wert belegt. Wenn man der Kette folgt, nehmen dann die Felder abwechselnd den einen oder anderen Kandidaten-Wert an, z.B. haben Feld 1 der Kette und Feld 3 einer solchen Kette immer den gleichen Wert. (Dies wurde in Strategie 11 benutzt.) Nimmt man dagegen dagegen einen ungeraden Abstand zwischen den Feldern in der Kette wie z.B. 1 oder 3, nehmen die Felder immer den anderen Kandidaten-Wert an. (Der Abstand 1 wurde in Strategie 5 eingesetzt.)

Konkret heißt das, dass wenn in Feld 1 der eine Kandidaten-Wert steht im Feld 2,4 ... der Kette der andere stehen muss.

Damit kann man feststellen, dass in den Feldern, die von diesen Feldern gemeinsam beeinflusst werden - die Schnittmenge ihrer Bedingungsumfelder - diese beiden Kandidaten-Werte der Kette nicht stehen können und damit als Kandidaten gestrichen werden können.

Damit eine solche Kette eingesetzt werden kann, müssen 3 Bedingungen erfüllt sein:

• die benachbaren Felder der Kette sind jeweils über ein Bedingungsumfeld verbunden
• die Felder der Kette müssen alle die gleichen zwei Kandidaten haben
• die Kette muss eine gerade Anzahl von Elementen haben (Strategie 5 ist der Spezialfall einer Kette mit zwei Elementen).

Im Beispiel bilden die orangen Felder S7R5, S2R5, S2R8 und S3R9 eine solche Kette. Nimmt S7R5 den Wert 2 an, hat S3R9 den Wert 8.

VIEL THEORIE !!!

die Kette

In dem Beispiel besteht die Kette aus den orangen Feldern S7R5, S2R5, S2R8 und S3R9 mit dem gemeinsamen Kandidaten-Werten 2 und 8.

die Logik

In allen Felder, die die beiden Felder an den Enden der Kette gemeinsam beeinflussen können die Werte 2 und 8 nicht stehen.

das Resultat

Das Feld, in dem die Kandidaten-Werte 2 und 8 ausgeschlossen wurden (S7R9), ist blau gekennzeichnet.

Auf das Bild KLICKEN um es zu vergrößern!

Seitenanfang

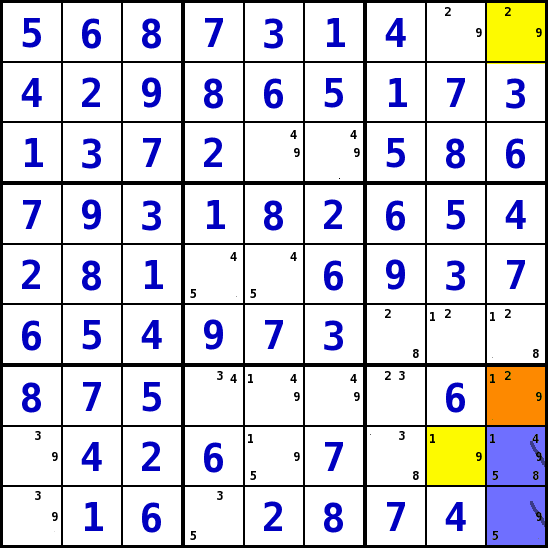Erweiterte XYWing-Strategie: XYZWing (Strategie 13)

Die Logik der Idee dieser Strategie ist mit der Strategie XYWing (11) weitgehend identisch, jedoch wird das mittlere Feld (der Connector) jetzt ein Feld mit drei Kandidaten-Werten. Die beiden äußeren Felder (die Flügel) haben je zwei Werte gemeinsam mit dem Connector und einen Wert miteinander gemeinsam.

Wenn als der Connector die Werte 3 , 4 und 5 als Kandidaten hätte, müsste zum Beispiel der eine Flügel die Kandidaten 3 und 4 der andere die Kandidaten 4 und 5 haben.

Von Interesse ist der Wert den die beiden Flügel gemeinsam mit dem Connector haben , in unserem Beispiel oben der Wert 4. Dieser Wert muss in einem dieser drei Felder sein, wenn die beiden Flügel über je eine Bedingungsumfeld mit dem Connector verbunden sind.

Damit kann man sagen, dass in allen Feldern, auf die diese 3 Felder Einfluss haben - die Schnittmenge der Bedingungsumfelder -, der gemeinsame Wert dieser drei Felder nicht vorkommen kann.

Damit eine solche Kombination zu neuen Erkenntnissen führt, müssen folgende Voraussetzungen erfüllt seien:

• die Flügel haben ein gemeinsames Bedingungsumfeld mit dem Connector
• die Fügel haben kein gemeinsames Bedingungsumfeld
• alle drei Felder haben einen gemeinsamen Kandidaten.
• die Flügel haben je einen unterschiedlichen gemeinsamen Kandidaten mit dem Connector
• der Connector hat 3 Kandidaten-Werte, die Fügel je 2 Kandidaten-Werte.

VIEL THEORIE !!!

der Connector

In dem Beispiel ist der Connector das Feld S9R7 (orange). Kandidaten : 1, 2, 9

die Flügel

Flügel sind die Felder S9R1 (Kandidaten 2, 9) und S8R8 (Kandidaten 1, 9) (gelb)

der gemeinsame Wert

Der Wert 9 ist der gemeinsame Kandidaten-Wert der drei Felder.

das Resultat

Die Felder, die von allen drei Feldern gemeinsam beeinflusst werden sind blau gekennzeichnet (S9R8, S9R9). In diesen kann man den Wert 9 als Kandidaten streichen.

Auf das Bild KLICKEN um es zu vergrößern!

Seitenanfang

Strategien mit fünf Feldern und fünf Werten (Strategie 14)

Diese Strategie ist die Fortsetzung der Strategien von level 7 mit einer von vier auf fünf erhöhten Zahl. Es ist jedoch so, dass dieses nicht vorkommen kann, da die restlichen Felder dann eine Kombination von vier Werten mit vier Feldern bilden. Wie die Statistik auf der rating-Seite zeigt, kommt es auch nicht vor.

Seitenanfang

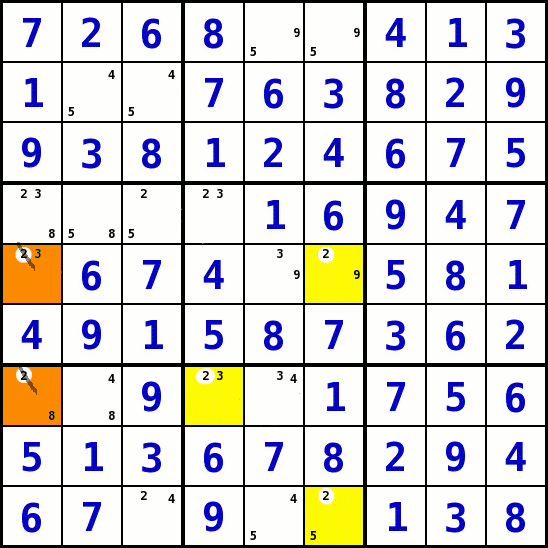Ketten für einen Kandidatenwert mit ungerader Länge: OddChain (Strategie 15)

Die Idee nimmt sich die Kandidaten-Werte vor, die in einem Bedingungsumfeld nur in zwei Feldern vorkommen. Ausgangspunkt der Überlegungen ist die Tatsache, dass eines dieser beiden Felder diesen Wert am Ende annehmen muss.

Man sucht auf dem Spielfeld nach mehreren solchen Kombinationen für einen Wert. Kombiniert man jetzt für einen Kandidaten-Wert diese Felder so, dass dass eine Kette entsteht, d.h. das eine Feld im einen Bedingungsumfeld ist auch in einer Kombination eines anderen Bedingungsumfeldes enthalten. Damit entsteht eine Kette, in der der gewählte Kandidaten-Wert entweder in den ungeraden Gliedern der Kette oder in den geraden steht.

Wichtig ist nun dass der Anfang einer Kette und das Ende der Kette in einem gemeinsamen Bedigungsumfeld stehen. Wenn die Kette eine ungerade Anzahl von Gliedern (Feldern) hat, nehmen entweder die beiden Kettenglieder an den beiden Enden der Kette den Kandidaten-Wert an - was nicht möglich ist, wenn sie ein gemeinsames Bedigungsumfeld haben - oder keines der beiden Felder nimmt den Wert an - was möglich ist .

Damit kann man schließen, dass der Kandidaten-Wert in dem Start- und dem Ende-Feld der Kette nicht möglich ist.

Damit eine solche Kombination zu neuen Erkenntnissen führt, müssen folgende Voraussetzungen erfüllt seien:

• ein Kandidaten-Wert muss in mehreren Bedingungsumfeldern jeweils nur in zwei Feldern möglich sein.
• die Verbindung der Kette wird über Felder realisiert, die in zwei Bedingungsumfeldern in einer solchen Zweier-Kombination enthalten sind
• die Kette muss eine ungerade Anzahl von Feldern enthalten
• das Anfangs- und Endfeld müssen ein gemeinsames Bedingungsumfeld haben

VIEL THEORIE !!!

das Anfangsfeld

In dem Beispiel ist das Feld S1R5 (orange) das Anfangsfeld. Es ist mit dem Feld S6R5 darüber verbunden, dass der Wert 2 in dieser Reihe (5) nur in diesen beiden Felder vorkommen darf.

die Kette

Die Kette geht dann von S6R5 zu S6R9 - auch hier kann der Wert 2 nur in diesen beiden Feldern sein.
S6R9 ist verbunden mit S4R7 , da in dem gemeinsamen Block (8) der Wert 2 nur in diesen Feldern stehen kann.

das Endfeld

Vom Feld S4R7 geht es zum Endfeld S1R7. Auch hier kann der Wert 2 nur in einem der Felder stehen.

die Verbindung

Das Start und das Endfeld haben die Spalte 1 als gemeinsames Bedingungsumfeld.

das Resultat

Würde man im Startfeld (S1R5) den Wert 2 einsetzen, würde auch im Endfeld der Wert 2 stehen müssen:
S1R5 ist 2 => S6R5 = nicht 2 => S6R9 = 2 => S4R7 = nicht 2 => S1R7 = 2
Dies ist aber nicht möglich, da beide ein gemeinsames Bedingungsumfeld haben.
Damit steht fest, dass der Wert 2 nicht im Start- oder Endfeld stehen kann.

Auf das Bild KLICKEN um es zu vergrößern!

Seitenanfang